Почему перпендикулярные прямые не пересекаются — объяснение
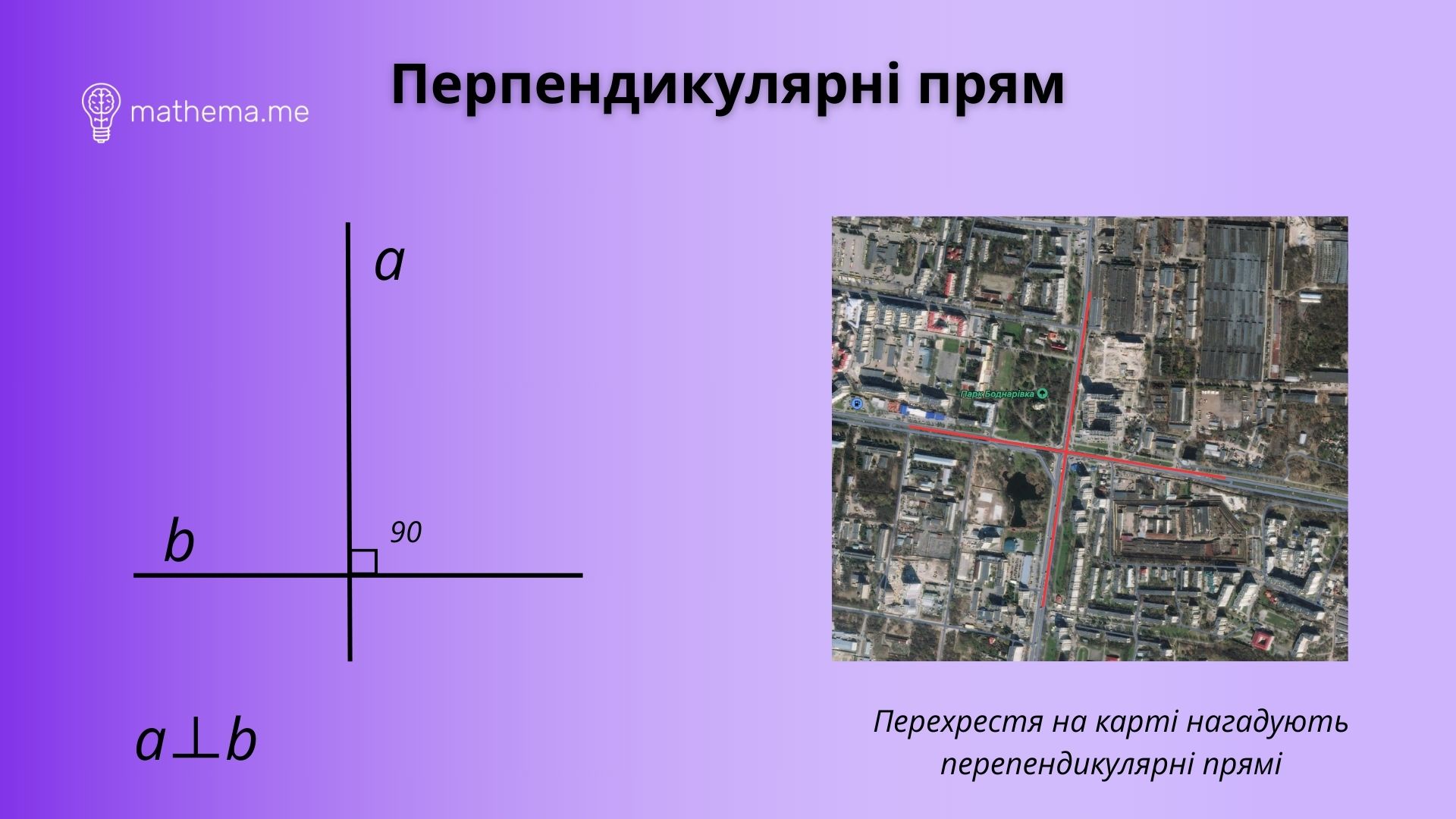
Одно из фундаментальных свойств геометрии – перпендикулярные прямые. Эти прямые, образующие угол в 90 градусов друг с другом, имеют особое положение и важные свойства. Одним из таких свойств является то, что перпендикулярные прямые никогда не пересекаются. В этой статье мы разберем, почему это так и как можно объяснить данное явление.
Перпендикулярные прямые не пересекаются из-за особого расположения их углов. Для того чтобы две прямые пересекались, их углы должны быть меньше или больше 90 градусов. Если угол между двумя прямыми равен 90 градусам, то они перпендикулярные и не пересекаются.
Это можно объяснить геометрически. Представьте, что наша плоскость – это лист бумаги или стол. Если мы возьмем две ручки и нарисуем на этом листе две прямые, образующие угол в 90 градусов, то легко увидим, что они никогда не смогут пересечься. Они просто не имеют возможности сблизиться достаточно близко, чтобы пересечься.
Таким образом, перпендикулярные прямые представляют особую конфигурацию в геометрии, где угол между ними равен 90 градусов. Из-за этого особого положения углов, перпендикулярные прямые никогда не пересекаются. Это свойство имеет важное применение во многих областях, таких как архитектура, инженерия и дизайн.
Геометрическое объяснение
Перпендикулярные прямые не пересекаются в геометрии в силу свойств углов и отношений сторон.
Представим, что у нас есть две прямые, которые перпендикулярны друг другу. Мы можем представить каждую из них как бесконечно длинную линию, которая протянута в определенном направлении. Когда эти две прямые пересекаются, они образуют угол и две соответствующие стороны.
Если прямые перпендикулярны, то они будут образовывать прямой угол, то есть угол, равный 90 градусам. В прямом угле две стороны являются перпендикулярными друг другу и, следовательно, параллельны. Таким образом, при пересечении перпендикулярных прямых образуется два параллельных участка, которые не могут пересечься, поскольку они не имеют общей точки.
В геометрии перпендикулярность играет важную роль, так как это свойство позволяет строить прямые углы, что является основой для измерения углов и создания геометрических форм.
Итак, геометрический аргумент объясняет, что перпендикулярные прямые не пересекаются, потому что они образуют прямой угол и две параллельные стороны.
Свойства перпендикулярных прямых
1. Угол между перпендикулярными прямыми равен 90 градусов. Одно из основных свойств перпендикулярных прямых заключается в том, что угол между ними всегда равен 90 градусов. Это обозначает, что они пересекаются под прямым углом и их направления взаимно перпендикулярны.
2. Произведение коэффициентов наклона перпендикулярных прямых равно -1. Если у нас есть две перпендикулярные прямые, то их коэффициенты наклона являются различными и взаимно обратными. Произведение этих коэффициентов всегда будет равно -1. Например, если одна прямая имеет наклон 2, то вторая прямая будет иметь наклон -1/2.
3. Уравнения перпендикулярных прямых имеют противоположные знаки перед коэффициентами наклона. Когда мы записываем уравнения перпендикулярных прямых, то у коэффициента наклона одной прямой будет противоположный знак по сравнению с коэффициентом наклона другой прямой. Например, если у первой прямой уравнение имеет вид y = 2x + 3, то у второй прямой уравнение будет выглядеть как y = -2x + b.
4. Перпендикулярные прямые относятся к разным семействам прямых. Перпендикулярные прямые принадлежат к разным семействам прямых. Например, одна из прямых может принадлежать семейству прямых, заданных уравнением y = mx + b, а вторая прямая будет принадлежать семейству прямых, заданных уравнением y = -1/mx + c. Это связано с тем, что угол наклона перпендикулярных прямых всегда отличается, поэтому они принадлежат к разным типам прямых.
Перпендикулярные прямые играют важную роль в геометрии и алгебре. Знание и понимание их свойств помогает в решении различных задач и построении геометрических фигур.
Угол между перпендикулярными прямыми
| Перпендикулярные прямые | Угол между ними |
|---|---|
| Прямые, которые пересекаются под прямым углом | 90 градусов |
| Прямая, перпендикулярная оси абсцисс, и прямая, перпендикулярная оси ординат | 90 градусов |
Угол между перпендикулярными прямыми является одним из основных свойств таких линий. Это свойство обеспечивает уникальность перпендикулярных прямых и различие их от других типов прямых, которые могут образовывать углы разного размера и ориентации.
Алгебраическое объяснение
Перпендикулярные прямые не пересекаются в двумерном пространстве. Это может быть объяснено с помощью алгебраических свойств углов, наклона и уравнений прямых.
Для начала, рассмотрим угол между двумя прямыми. Если угол между прямыми равен 90 градусов, то они будут перпендикулярными.
В алгебраическом плане, уравнения перпендикулярных прямых имеют следующий вид:
| Уравнение прямой | Угловой коэффициент (наклон) |
|---|---|
| y = mx + b | m |
| y = (-1/m)x + b | -1/m |
В таблице представлены уравнения прямых вида y = mx + b, где m — наклон прямой, а b — свободный коэффициент (смещение по y-оси).
Если две прямые перпендикулярны, то их угловые коэффициенты должны обладать таким свойством: m * (-1/m) = -1. То есть, произведение угловых коэффициентов должно быть равно -1.
Но, если у двух прямых угловые коэффициенты равны, то произведение m * m = m^2. При любом значении m (кроме случая m = 0) произведение m^2 не будет равно -1.
Из алгебраического обоснования следует, что перпендикулярные прямые не пересекаются, так как их угловые коэффициенты не могут быть равными.
Уравнения перпендикулярных прямых
Пусть дана прямая L1 со следующим уравнением: y = mx + b. Здесь m — угловой коэффициент прямой, а b — свободный член. Чтобы найти уравнение L2 перпендикулярной прямой к L1, нам необходимо поменять знак углового коэффициента m на противоположный и добавить его в уравнение L1. Представим уравнение перпендикулярной прямой L2 в следующем виде: y = -mx + d. Здесь d — новый свободный член.
Итак, мы видим, что уравнение прямой L2 получается из уравнения прямой L1 путем замены знака углового коэффициента m на противоположный и изменения свободного члена. Это свойство позволяет нам легко находить уравнения перпендикулярных прямых и использовать их для решения различных задач и задач геометрии.
Система уравнений перпендикулярных прямых
Пусть уравнение первой прямой задано в виде y = mx + b, где m — это угловой коэффициент и b — это коэффициент смещения по оси y.
Уравнение второй перпендикулярной прямой может быть записано в виде y = -1/mx + b’, где b’ — это новый коэффициент смещения по оси y.
Из данной системы уравнений видно, что угловые коэффициенты двух перпендикулярных прямых являются обратными величинами, т.е. если у первой прямой m = 0, то у второй прямой m’ = -1/0 = +/-∞.
Таким образом, перпендикулярные прямые не пересекаются и параллельны оси y или оси x в зависимости от их углового коэффициента.
Система уравнений перпендикулярных прямых играет важную роль в геометрии и различных областях науки и техники, где требуется точное определение взаимного расположения прямых и плоскостей.
Практическое применение перпендикулярных прямых
Перпендикулярные прямые играют важную роль в различных областях нашей жизни, где требуется точное измерение и построение прямых линий.
Одним из практических применений перпендикулярных прямых является строительство и архитектура. Перпендикулярные линии используются для создания прямых углов и определения перпендикулярности стен и других строительных элементов. Благодаря этому, строительство становится более точным и устойчивым.
Еще одним примером практического применения является геометрия и измерение расстояний. Для измерения вертикальных и горизонтальных линий используются перпендикулярные прямые, что позволяет получить более точные и надежные результаты.
Перпендикулярные прямые также находят применение в навигации и картографии. Путем использования перпендикулярных линий можно точно определить направление и координаты объектов на карте, что помогает мореплавателям и путешественникам ориентироваться в пространстве и находить нужное направление.
Кроме того, перпендикулярные прямые используются в радиоинженерии и электронике. Они служат для создания антенн и других электронных устройств, которые требуют точной ориентации и высокой производительности.
Использование перпендикулярных прямых в различных областях нашей жизни позволяет улучшить точность и эффективность работы, а также создать устойчивые и надежные конструкции. Поэтому понимание перпендикулярности и умение работать с перпендикулярными линиями является неотъемлемой частью современного образования и профессиональной деятельности.
Применение в архитектуре и строительстве
Концепция перпендикулярных прямых, которые не пересекаются, имеет важное значение в архитектуре и строительстве.
Одной из основных применений перпендикулярных прямых является использование их для создания прямых углов в строительстве. В архитектуре перпендикулярность применяется для расположения стен, окон, дверей и других элементов здания. Когда сооружение имеет прямые углы, оно выглядит более симметрично и эстетично.
Другое важное применение перпендикулярных прямых в архитектуре связано с созданием фундамента и строительными измерениями. При проектировании и строительстве здания часто требуется точное определение перпендикулярности для обеспечения стабильности и надежности конструкции.
Перпендикулярные прямые также используются в архитектурных чертежах и планах для указания расположения объектов. Они служат важным инструментом для архитекторов и строителей, помогая им устанавливать пропорции и располагать элементы здания в соответствии с заданными параметрами.
В строительстве техническое измерение перпендикулярных прямых играет важную роль при установке фундамента, стен, потолков и других конструкций. Точность и качество строительства напрямую зависят от правильного определения перпендикулярности.
Таким образом, понимание концепции перпендикулярных прямых и их применение в архитектуре и строительстве позволяют создавать красивые, функциональные и устойчивые сооружения.
Вопрос-ответ:
Почему перпендикулярные прямые не пересекаются?
Перпендикулярные прямые не пересекаются потому, что они имеют угол между собой 90 градусов. Такой угол образуется только тогда, когда одна прямая перпендикулярна другой, то есть они взаимно перпендикулярны. Если бы перпендикулярные прямые пересекались, то между ними образовался бы угол, который не был бы равен 90 градусам, а это противоречило бы определению перпендикулярности.
Нужно ли чтобы перпендикулярные прямые имели одинаковую длину?
Нет, для того чтобы две прямые были перпендикулярными, не требуется, чтобы они имели одинаковую длину. Они могут иметь разные длины, но при этом должны пересекаться и образовывать угол в 90 градусов. Длины перпендикулярных прямых могут быть разными и зависят от их положения в пространстве.
Может ли перпендикулярная прямая пересекать плоскость?
Перпендикулярная прямая может пересекать плоскость. Перпендикулярность означает, что угол между прямой и плоскостью равен 90 градусам. Поэтому перпендикулярная прямая может пересекать плоскость в точке или быть полностью лежащей в одной из плоскостей, параллельных данной плоскости.
В чем отличие перпендикулярных прямых от параллельных?
Перпендикулярные прямые имеют угол между собой 90 градусов и пересекаются. Параллельные прямые не пересекаются и не имеют общей точки. Они лежат в одной плоскости и имеют одинаковый угол наклона. Перпендикулярные прямые можно встретить в пространстве или на плоскости, а параллельные прямые чаще всего встречаются на плоскости.
Как можно проверить, что две прямые перпендикулярны друг другу?
Для проверки перпендикулярности двух прямых можно воспользоваться теоремой Пифагора. Если мы знаем длины отрезков, которые образуют прямые, то можно проверить, что квадрат суммы этих длин равен квадрату длины гипотенузы, образованной перпендикулярными прямыми.